Probability versus Odds I keep referencing the odds and logodds as ways to express probability, so it's worth the time to explain this concept by itself In the future I can reference this post rather than reexplain the same idea every time Probabilities are numbers between zero and one 0,1 This is sometimes also expressed as aOften 'odds' are quoted as odds against, rather than as odds in favor For example, the probability that a random day is a Sunday is oneseventh (1/7), hence the odds that a random day is a Sunday are 1 6 The odds against a random day being a Sunday are 6 1Implied Probability = (1*(Odds)) / (1(Odds) 100) Which looks like Implied Probability = (1*(110)) / (1(110) 100) or 524% or 0524 = 110 / 210

Probability And Odds Youtube
What is the difference between odds and chances
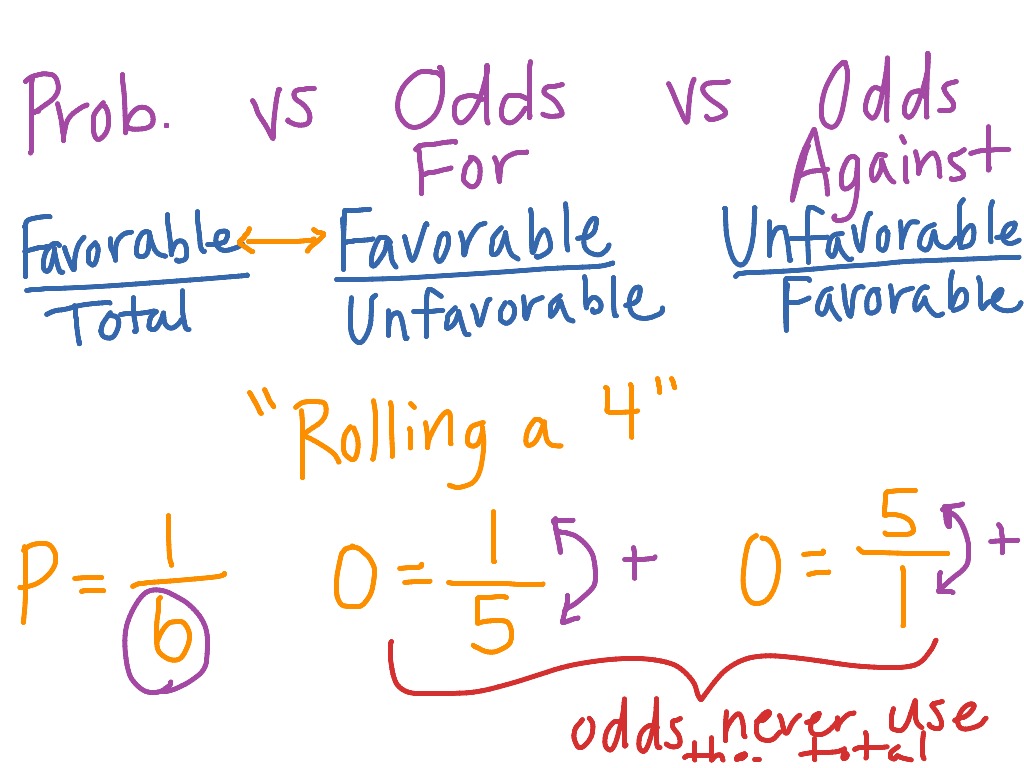
What is the difference between odds and chances- Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen Odds in favor of A = A / (1 A), usually simplified to lowest terms, For instance, if the probability of an event occurring is 075, then the odds for it happening are 075/025 = 3/1 = 3 to 1 for, while the probability that it doesn't occur is 1 to 3 against Odds vs Probability When you're talking about the likelihood of something happening, it's easy to confuse odds and probability People define the odds as the probability that something happens divided by the probability that it doesn't happen Knowing the odds of an event happening is an excellent way to check the outcome you want




Probability
Labs(title ="probability versus odds") 000 025 050 075 100 0 50 100 150 odds p probability versus odds Finally, this is the plot that I think you'llfind mostHome > Online Casinos > Casino Articles > House Odds vs True Odds House Odds vs True Odds I've written about house odds vs true odds before, but not in so many words You can read about the basics of probability on this site, and you can read about the house edgeBut another way of looking at these concepts is by examining the difference between payoff odds and true oddsOdds The odds in favor of an event is the ratio of the number of ways the outcome can occur to the number of ways the outcome cannot occur # of ways the event CAN occur # of ways the event CANNOT occur This is actually a lot easier than
In everyday conversation when numbers or values aren't given, the two terms are synonymous If an event has a high probability, then it has high odds for happening The incorrect usage arises when a person ascribes a mathematical value toOdds are based on the probability that an event will ever occur 2 Probability only measures the chances that an event will occur against the total number of times the even will occur; The odds are 1626 and probability is 016% If you're playing poker long enough you will somewhat regularly encounter the aces vs kings scenario at a table A formula to estimate the probability for this to happen at a 9 player table is This formula slightly underestimates the actual probability which is a little bit higher
Many people wrongfully assume odds and probabilities are the same thingThey're definitely not, as there's a significant difference between saying there are In contrast, probability lies between zero to one Therefore, the closer the probability to zero, the more are the possibilities of its nonoccurrence, and the closer it is to one, the higher are the possibilities of the event Odds are the ratio of positive events to negative events In this matchup, there is a big difference between the two odds, indicating a much higher probability of Duke winning the game and advancing to the




Binary Logistic Regression With Odds Ratios Calculated For The Download Table
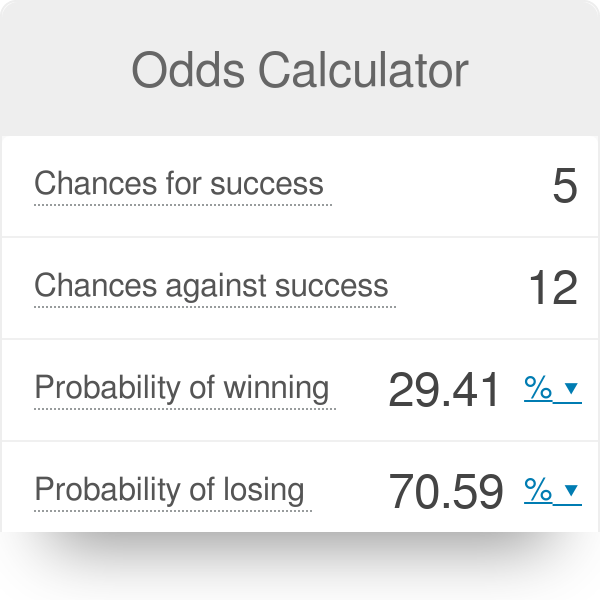



Odds Calculator
Probability of Winning = () or % Losing = () or % Odds ratio vs probability ratio Ask Question Asked 1 year, 8 months ago Active 7 months ago Viewed 647 times 8 5 $\begingroup$ An odds is the ratio of the probability of an event to its complement $$\text{odds}(X) = \frac{P(X)}{1P(X)}$$ An odds ratio (OR) is Odds, chances and probability are just different ways of expressing the likelihood of an event In your example of the jackpot that hits on average once per 100,000 spins, the probability of hitting the jackpot is Many people have difficulty relating to a decimal number So another, equivalent way to express the likelihood of hitting




Lecture 5 Basic Probability David R Merrell Intermediate Empirical Methods For Public Policy And Management Ppt Download




Odds And Likelihood Ratios Likelihood Ratios Can Help In By Anthony B Masters Oct 21 Medium
Using an example of decimal odds, a candidate has 2 odds to win the next election If so, the implied probability is 4545%, or ( 1 2 2 × 1Odds of not drawing a 6 = 92 (Read as "9 to 2") P(winner) = number of plates number of winning plates _ _ _ _ _ = 25 1 The probability of having the winning plate is 1 out of 25 Odds of winning = number of chances to win number of chances to draw other numbers Odds of winning = 124 (Read as "1 to 24") The wikipedia page claims that likelihood and probability are distinct concepts In nontechnical parlance, "likelihood" is usually a synonym for "probability," but in statistical usage there is a clear distinction in perspective the number that is the probability of some observed outcomes given a set of parameter values is regarded as the likelihood of the set of parameter




Betting Odds And Breakeven Probability By Cary Mosley Medium




Probability And Odds Worksheet And Probability And Odds Worksheet Name Period Sammy Has A Number
Odds Odds seems less intuitive It is the ratio of the probability a thing will happen over the probability it won't In the spades example, the probability of drawing a spade is 025 The probability of not drawing a spade is 1 025 So the odds is 025/075 or 13 (or 033 or 1/3 pronounced 1 to 3 odds) Moving back and forth2 What is the probability of not spinning a yellow?7 What are the odds in favor of rolling a 6?




Bayes Rule Odds Form Intro Math 1 Arbital




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1
Probability of death is three times higher than the probability of surviving Table 2 gives the odds among men and women on the Titanic Table 2 Odds for death among men and women on the Titanic, ˇdenotes the probability of death Death Survival Sex ˇ 1 ˇ Odds men 079 021 376 women 027 073 037 If risk was the same in both groups, theAnswer (1 of 5) From a mathematics standpoint, let's assume p = number of possible positive outcomes of an event q = number of possible negative outcomes of an event Therefore p q = total number of outcomes of an event The probability of a positive event occurring is p3 What are the odds in favor of spinning a yellow?




Probability And Odds Youtube




Bayes Rule Odds Form Intro Math 1
In the lower, I varied the values of the p parameter The probability distribution function is4 What are the odds against spinning a yellow?6 What is the probability of not rolling a 6?




Math 30 2 Probability Odds Acceptable Standards 50 79 The Student Can Express Odds For Or Odds Against As A Probability Determine The Probability Ppt Download




True Odds Calculator Find Probabilities Fair Odds Margin
As you can see, the idea of probability is relatively simple But the idea of odds, on the other hand, is a bit more complicatedmostly because there's more than one way to write them The most common way is what's called "bookmakers odds" Packers vs Chiefs odds, spread, line, predictions NFL picks, Week 9 best bets from model on 126 run SportsLine's model simulated Kansas City Chiefs vs Green Bay Packers and made its NFL picks The term 'Odds' is commonplace, but not always clear, and often used inappropriately The odds of an event is the number of events / the number of nonevents This turns out to be equivalent to the probability of an event/the probability of a nonevent You'll often see odds written as P/(1P)



Odds Probability The Difference Explained With Examples



Ctspedia Ctspedia Oddsterm
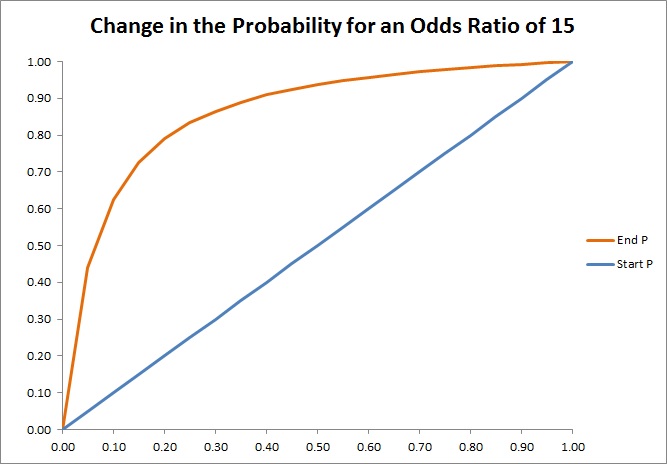
Odds ratios work the same An odds ratio of 108 will give you an 8% increase in the odds at any value of X Likewise, the difference in the probability (or the odds) depends on the value of X So if you do decide to report the increase in probability at different values of X, you'll have to do it at low, medium, and high values of X The differences between odds and probability are discussed in the points given below The term 'odds' is used to describe that if there are any chances of the occurrence of an event or not As against, While odds are expressed in the ratio, the probability is either written in percentage form or Example 3 Likelihood vs Probability in Gambling Suppose a casino claims that the probability of winning money on a certain slot machine is 40% for each turn If we take one turn , the probability that we will win money is 040 Now




Probability Vs Odds What S The Deal With State Lottery Odds Table




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science
How to find probability and odds and the difference between the two We also discuss experimental probablility, theoretical probability, odds in favor, andThe chance of winning is 4 out of 52, while the chance against winning is 48 out of 52 (524=48) Entering A=4 and B=48 into the calculator as 448 odds are for winning you get For 4 to 48 odds for winning; Figure 1 The binomial probability distribution function, given 10 tries at p = 5 (top panel), and the binomial likelihood function, given 7 successes in 10 tries (bottom panel) Both panels were computed using the binopdf function In the upper panel, I varied the possible results;




Ppt Odds And Probabilities Powerpoint Presentation Free Download Id




What Are The Odds That You Know About The Odds Analytics Vidhya
To convert odds to probability, take the player's chance of winning, use it as the numerator and divide by the total number of chances, both winning and losing For example, if the odds are 4 to 1, the probability equals 1 / (1 4) = 1/5 or % Odds of 1 to 1 (50%) are called "evens," and a payout of 1 to 1 is called "even money" I also explain the difference between probability and odds An Event's Probability Is Always a Ratio No matter what event you're looking at, it has a probability of occurring That probability is just a ratio measuring the number of ways that event can happen versus the number of ways it can't happenRISK AND ODDS DEFINITIONS "Risk" refers to the probability of occurrence of an event or outcome Statistically, risk = chance of the outcome of interest/all possible outcomes The term "odds" is often used instead of risk "Odds" refers to the probability of occurrence of an event/probability of the event not occurring




Odds Are Not The Same As Probabilities Will Townes




Finite Probability Spacea In A Swimming Race The Odds That A Will Win Are 5 Homeworklib
The odds of not rolling a 5 or 6 is the inverse 42 This is because there are 4 events that produce the specified outcome of "not rolling a 5 or 6" (rolling a 1,2,3, or 4) and two that do not (rolling a 5 or 6) The probability of an event is different, but related, and can be Summary 1 Probability is a mathematical measure of how often an event will occur; Odds Is Related to Probability The formal way to describe the odds is as the probability of the event divided by the probability of the nonevent So odds are the ratio of two fractions the number of events divided by the number of




7 Facts About Probability And Odds That You Don T Know



Worksheet Probability And Odds Number Cubes Dice Marbles Pre Algebra Printable
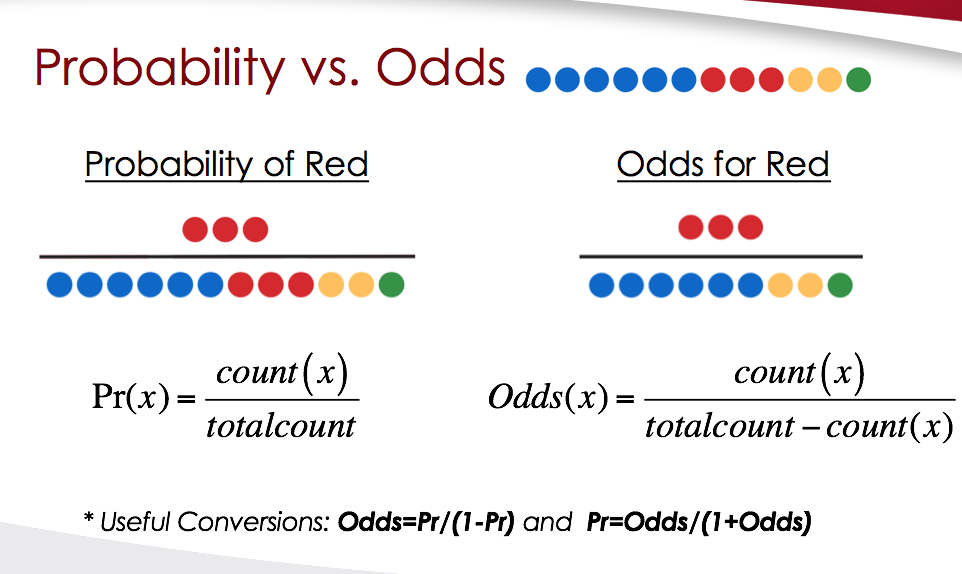
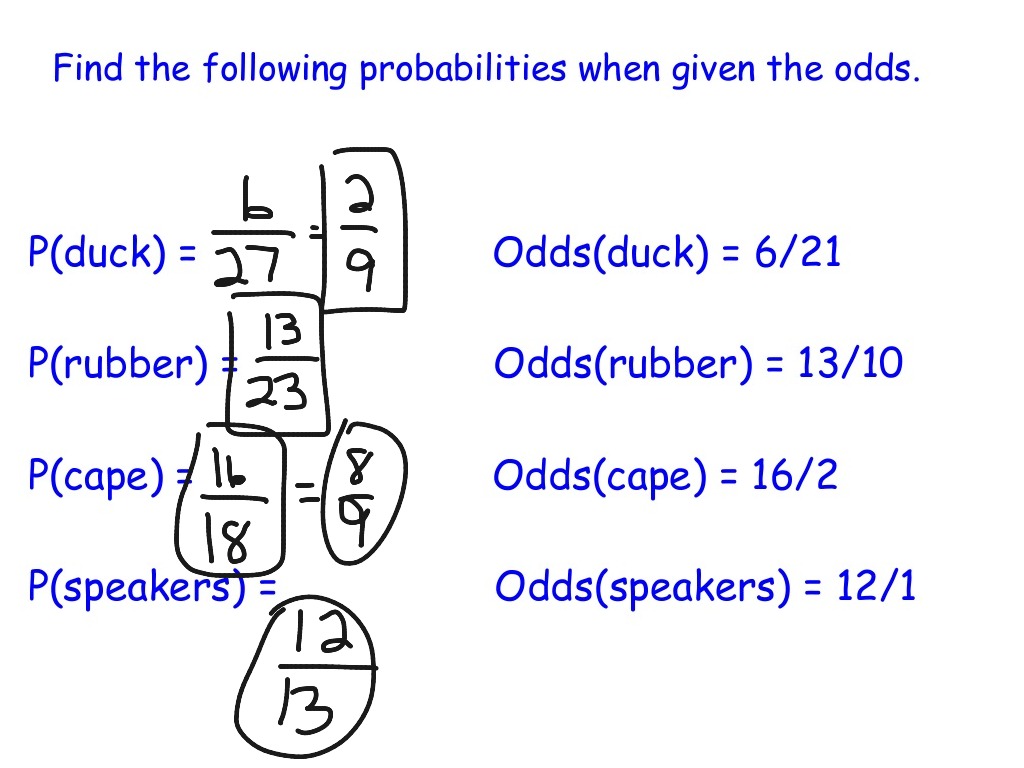
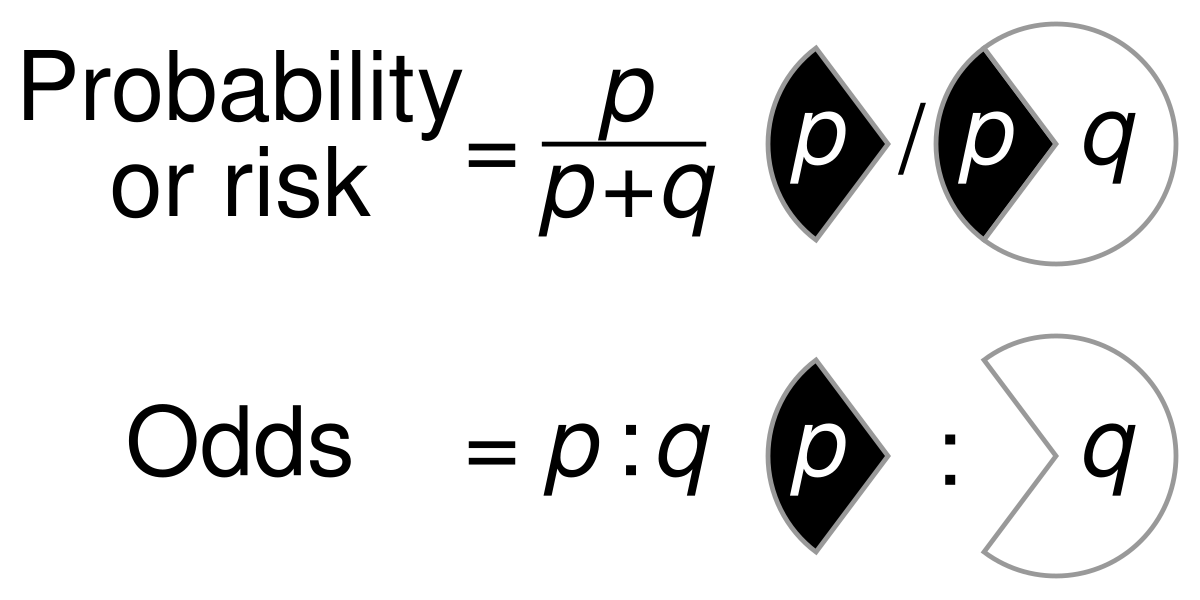
1The probability of a particular outcome from an event will lie between zero and one 2 The probability of an event that is certain to happen is equal to one For example, the probability that everybody dies eventually 3 The probability of an event that is impossible is zero For example, throwing a seven with a normal dice 4Probability/Odds Conversion Converting probabilities into odds, we simply divide the probability by 1 less the probability, eg, if the probability is 25% (025), the odds are 025/075, which can also be expressed as 1 to 3 or 1/3 or 0333 The Ask Dr Math forum has several entries on odds versus probability Summarizing, one way to conceptualize (nontechnically) the probability of an event is the number of ways that an event can occur divided by the total number of possible outcomes The probability of heads in a fair coin flip is 1/2 (50 percent)




Odds And Log Odds Clearly Explained Youtube



Probability Odds Lessons Blendspace
Sammy has a number cube (dice) Calculate the following 5 What is the probability of rolling a 6?Equally, backing something at short odds with a potentially high probability does not guarantee it will become true As we have suggested, bookmakers use odds to display the probability or otherwise of all outcomes on sporting events They can do this in one of three ways fractional eg 2/1, decimal eg 300 or American eg 0 Odds can be helpful when we want to compare how much larger one probability is relative to another An event with a probability 75% has odds of 75 to 25 We can simplify this to 3 to 1 This means that the event is three times more likely to occur than not occur Cite this Article




Probability Vs Odds Math Probability Showme



Introduction To Probability And Odds Acu Mathcasts
Pretest probability and posttest probability (alternatively spelled pretest and posttest probability) are the probabilities of the presence of a condition (such as a disease) before and after a diagnostic test, respectively Posttest probability, in turn, can be positive or negative, depending on whether the test falls out as a positive test or a negative test, respectivelyFirst, we have a simple calculator that you can use to plug in any moneyline (American style odds) and quickly get the fair market probability that it implies We've also included a chart below the calculator for reference, and to see how favorites and underdogs compare Money Line Calculator (Implied Probability)Odds measure the chances for and the chances against an event ever occurring 3 Probability




Comparing Probability Odds For And Odds Against Youtube




Medical Studies




Binary Logistic Regression With Odds Ratios Calculated For The Download Table




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science




Changing Probability To Odds Square Puzzle Activity By Caryn Loves Math




Probability Vs Odds In Favour Or Against An Event Examples Youtube




Relation Between Probability And Odds At Different Values Of Probability Download Scientific Diagram
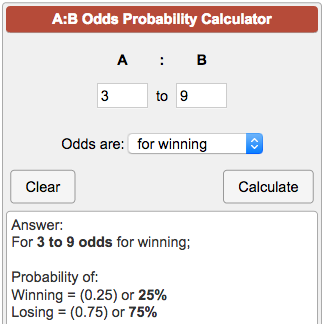



Odds Probability Calculator




Odds And Probability
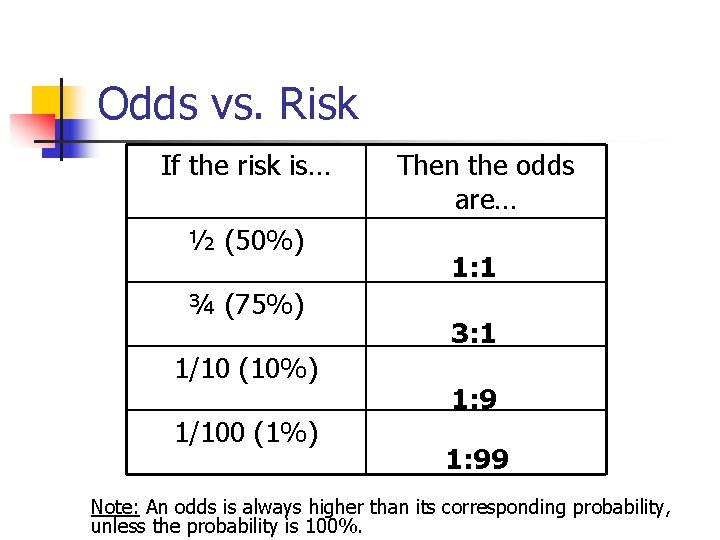



The Binomial Applied Absolute And Relative Risks Chisquare




Converting Between Probability And Odds Mathwoes Youtube



Odds Vs Risk Vantage Research




Poker Odds And Math Pokercalculatorreport Com




5 6 Probability And Odds Lesson
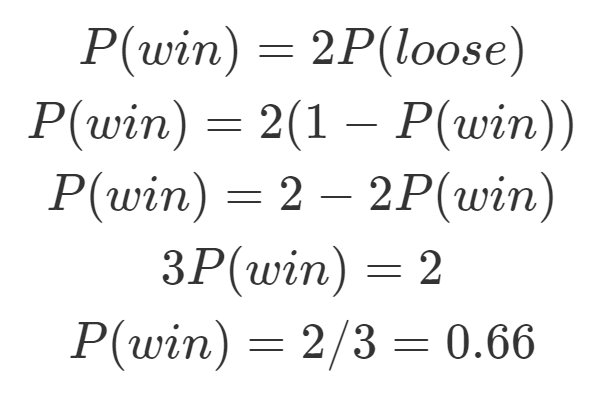



Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science
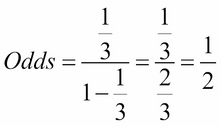



Probability Odds And Log Odds Principles Of Data Science



The Difference Between Probability And Odds




Independent Events Ck 12 Foundation




What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science



Odds Versus Probability Math Showme



Week 1 Data Acquisition Ebm Flashcards Memorang




Probability Probability Vs Odds Lesson Video By J Thompson Tpt




Probability Test Review What Are Your Chances Of Passing Ppt Download



Ctspedia Ctspedia Oddsterm




Probability Odds Odds Ratio Youtube




11 6 Probability Involving Or And Not



How To Convert Odds And Units To Probability Convert Odds To Percentage




Converting Probability To Odds Example Youtube




What Is An Odds Ratio And How Do I Interpret It Critical Appraisal




What S The Difference Between Probability And Odds




Probability




Difference Between Odds And Probability With Comparison Chart Key Differences




Section 11 6 Odds And Expectation Math In Our World Ppt Download



Odds Vs Probability Casino Spies




Odds Vs Probability What S The Difference Ask Difference




What Are The Odds That You Know About The Odds Analytics Vidhya



Probability Probability Vs Odds Lesson Math Statistics Showme




Odds Ratio The Odds Ratio Is Used To Find The By Analyttica Datalab Medium




England Vs Croatia Football Predictions And Betting Tips Crowdwisdom360



1



Odds Likelihood Ratios Guide To Diagnostic Tests




How To Calculate Odds 11 Steps With Pictures Wikihow




Odds And Probability



Probability Basics Laws Of Probability Odds And Probability




Odds And Probability Definitions Key Difference Between Odds And Probability Comparison Chart Examples Ccss Math Answers




9 2 Binary Logistic Regression R For Health Data Science



File Probability Vs Odds Svg Wikimedia Commons




What Are The Odds Stats With Cats Blog




Observed Versus Model Based Left Precipitation Probabilities Right Download Scientific Diagram




A Key Part Of Winning Bets The Math Behind Betting Odds Probability




Odds Ratios Versus Relative Risk




Probability And Odds Math Odds Showme




Combinatorics And Probability Pdf Odds Probability
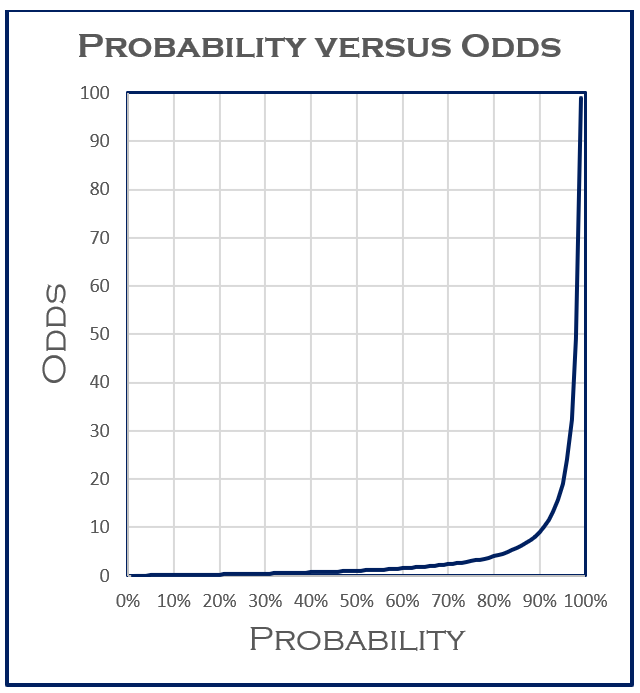



What Are The Odds Stats With Cats Blog




Sportsbetting Tips Understanding Probability
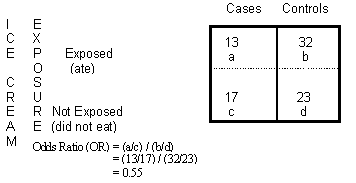



Odds Ratio Calculation And Interpretation Statistics How To




Statistics 12 Probability Vs Odds Stats Seandolinar Com



How To Calculate



Odds Vs Probability Vs Chance Data Science Central



Odds




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1
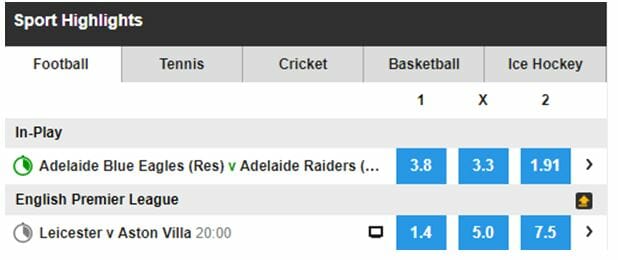



Implied Probability Betting Math Made Simple 21 Update




May The Odds Be In Your Favour Financially




Ppt Odds Vs Probabilities Powerpoint Presentation Free Download Id




Probability Vs Odds Youtube



1




Modelling Binary Logistic Regression Using Python One Zero Blog




Pdf Coherent Odds And Subjective Probability Semantic Scholar




Probability Chance And Odds Pdf Odds Probability




Webinar Recording Signup
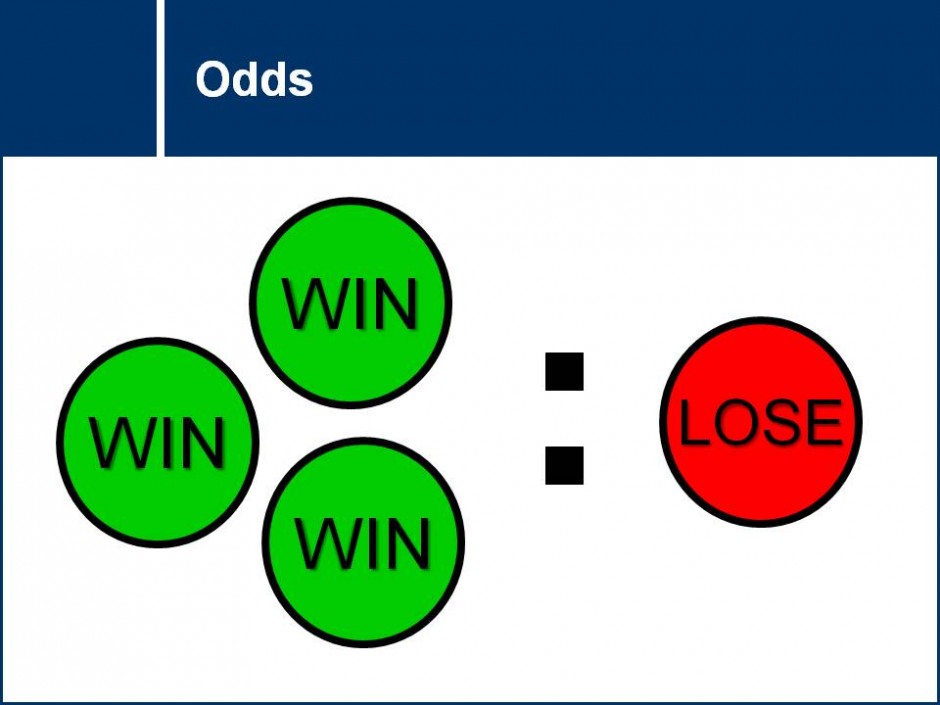



Statistics And Probability Mstltt




Simple Probability Definition Probability The Chance Some Event




Logistic Regression Univariate And Multivariate Between Probability Odds And Log Odds I You Can Use The Following Table To Compute One Measure Of Probability From Another P Odds Pdf Document




Probability And Odds By From The Hart 18 Teachers Pay Teachers




Part 3 Module 3 Probability Suppose We Create
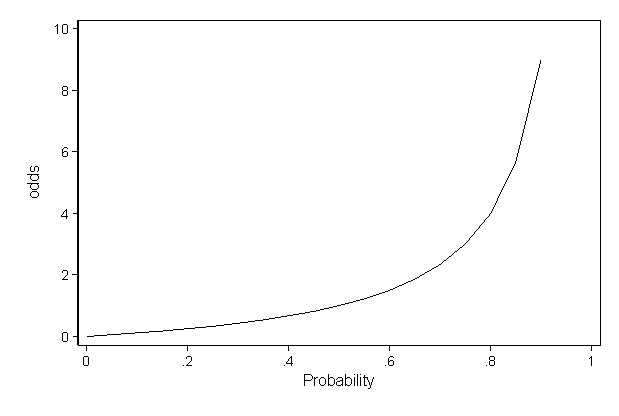



Faq How Do I Interpret Odds Ratios In Logistic Regression
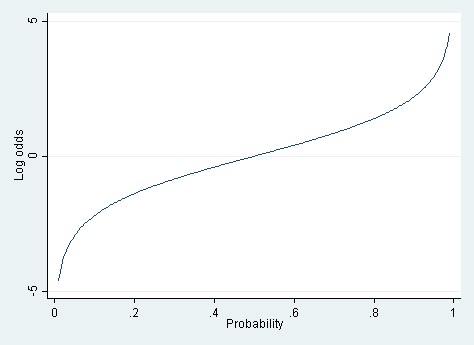



Linear Vs Logistic Probability Models Which Is Better And When Statistical Horizons



0 件のコメント:
コメントを投稿